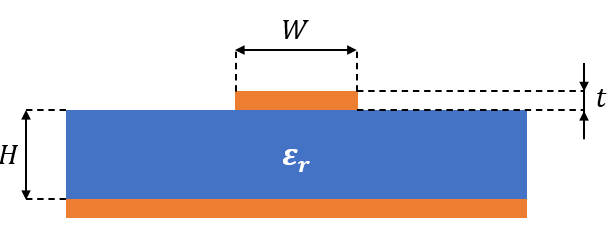
Microstrip lines are a type of transmission line used in microwave and RF (radio frequency) engineering for routing signals on printed circuit boards (PCBs) and integrated circuits (ICs). They are widely used due to their simplicity, ease of fabrication, and cost-effectiveness compared to other transmission line technologies like stripline or waveguides.
A microstrip line consists of a conducting traceon one side of a dielectric substrate, with a ground plane on the opposite side. The trace and ground plane are separated by the dielectric material, which provides electrical insulation and mechanical support.The characteristic impedance of a microstrip line depends on its dimensions, dielectric properties, and the relative permittivity of the substrate material. Typical characteristic impedance values range from 25 ohms to 100 ohms, but other values are possible depending on the design requirements. Microstrip lines are used in various RF and microwave circuits, such as antennas, filters, amplifiers, and interconnects within electronic systems. They are especially popular in PCB designs for high-frequency applications.
How to calculate its characteristic impedance?
The characteristic impedance (\(Z_0\)) of a microstrip line can be calculated using various empirical formulas or numerical methods. One commonly used empirical formula is the closed-form equation derived by Wheeler for calculating the characteristic impedance of a microstrip line. This formula provides a reasonably accurate approximation for typical microstrip line geometries. The Wheeler’s formula for microstrip characteristic impedance is given as:
\[
Z_0 = \frac{60}{\sqrt{\varepsilon_{\text{eff}}}} \ln\left(\frac{8h}{w} + \frac{w}{4h}\right)
\]
Where:
\( Z_0 \) = Characteristic impedance of the microstrip line (in ohms)
\( \varepsilon_{\text{eff}} \) = Effective dielectric constant of the microstrip line
\( h \) = Height of the dielectric substrate (thickness of the dielectric material above the ground plane, in meters or inches)
\( w \) = Width of the microstrip trace (in meters or inches)
The effective dielectric constant (\( \varepsilon_{\text{eff}} \)) takes into account the dielectric constant (\( \varepsilon_r \)) of the substrate material and the dimensions of the microstrip line. It can be approximated using the following formula:
\[
\varepsilon_{\text{eff}} = \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r – 1}{2} \left(1 + \frac{10h}{w}\right)^{-1/2}
\]
After calculating \( \varepsilon_{\text{eff}} \) using the above formula, you can substitute it back into the Wheeler’s formula to find the characteristic impedance \( Z_0 \).
Here’s a step-by-step guide to calculate the characteristic impedance of a microstrip line using Wheeler’s formula:
Measure or determine the relevant parameters:
– Dielectric constant (\( \varepsilon_r \)) of the substrate material.
– Height (\( h \)) of the dielectric substrate.
– Width (\( w \)) of the microstrip trace.
Calculate the effective dielectric constant \( \varepsilon_{\text{eff}} \) using the formula:
\[
\varepsilon_{\text{eff}} = \frac{\varepsilon_r + 1}{2} + \frac{\varepsilon_r – 1}{2} \left(1 + \frac{10h}{w}\right)^{-1/2}
\]
Substitute \( \varepsilon_{\text{eff}} \) into Wheeler’s formula to find the characteristic impedance \( Z_0 \):
\[
Z_0 = \frac{60}{\sqrt{\varepsilon_{\text{eff}}}} \ln\left(\frac{8h}{w} + \frac{w}{4h}\right)
\]
Calculate \( Z_0 \) using the values obtained in steps 1-
It’s important to note that while Wheeler’s formula provides a good approximation, it may not be suitable for extremely wide or narrow microstrip lines or for substrates with very high dielectric constants. In such cases, numerical methods or advanced electromagnetic simulation tools may be necessary for accurate characterization.
How to determine the trace width according to impedance and dielectric material height?
Assuming an infinitely thin line conductor, we can write for `w/h<=2`
`w/h=(8e^A)/(e^(2A)-2)`
where the factor A is given by
`A=Z_0/60 sqrt((epsilon_r+1)/2)+(epsilon_r-1)/(epsilon_r+1)(0.23+0.11/epsilon_r)`
For `w/h>=2`, we obtain
`w/h=2/pi{B-1-ln(2B-1)-(epsilon_r-1)/(2 epsilon_r)[ln(B-1)+0.39-0.61/epsilon_r]}`
where the factor B is given by
`B=(60pi^2)/(Z_0 sqrt(epsilon_r))`
These empirical formulas provide better accuracy compared to simpler approximations like the Hammerstad and Jensen formula, especially for microstrip lines with higher characteristic impedances or when more precise estimations are required. However, it’s important to note that even these formulas are approximations and may not always yield exact results, particularly for very specific substrate materials or complex geometries.
For critical designs or when exact impedance control is necessary, electromagnetic simulation tools or numerical methods are recommended. However, empirical formulas can serve as useful starting points or for rough estimations in preliminary design stages.