Finite Element Method (FEM) software often provides results in Cartesian coordinates due to its inherent computational approach. The FEM breaks down complex problems into smaller, manageable elements, typically triangles or quadrilaterals in 2D or tetrahedra and hexahedra in 3D. These elements are defined by their vertices and edges, forming a mesh that covers the entire domain of interest.
When solving physics-based problems using FEM, such as structural mechanics, heat transfer, or electromagnetics, the equations are formulated and solved in the local coordinate systems of these elements. In the case of electromagnetic analysis, for instance, the software computes the electric field components (Ex, Ey, Ez) at each element’s nodes or integration points.
Since the FEM naturally operates in the local coordinate systems of its elements, which are often Cartesian (x, y, z), the computed results are also provided in these Cartesian coordinates. This is convenient for visualizing and analyzing the results in a familiar coordinate system, making it easier for engineers and scientists to interpret and utilize the data.
However, it’s important to note that FEM software can also handle problems involving non-Cartesian coordinate systems. For example, in COMSOL Multiphysics and other advanced FEM packages, users can define and work with coordinate systems such as cylindrical or spherical coordinates for specific applications, such as rotating machinery, geophysical modeling, or spherical antennas.
FEM software primarily provides results in Cartesian coordinates due to the computational framework of the method itself. However both the normal and tangential components of a vector, such as the electric field in electromagnetics, play crucial roles in different contexts within physics and engineering.
The normal component of a vector is perpendicular to the surface under consideration. One scenario where the normal component is important is in understanding boundary conditions. For instance, when modeling electromagnetic wave propagation, specifying the normal component of the electric field at a boundary surface helps define how the field interacts with the boundary, whether it’s reflected, absorbed, or transmitted. This is fundamental in designing devices like antennas and waveguides, where controlling boundary interactions is critical for optimal performance.
The normal component is also essential in analyzing surface charge distributions. Gauss’s law relates the normal electric field component to the charge density on a surface, making it invaluable for understanding the behavior of charges on conductors or dielectric interfaces. In electrostatics, studying the normal component helps determine electric flux, potential distributions, and capacitance, aiding in the design of capacitors, insulating materials, and electrical systems.
On the other hand, the tangential component of a vector is parallel to the surface under consideration. One key application of the tangential component is in wave propagation phenomena. In optics, analyzing the tangential electric field component is crucial for understanding reflection, refraction, and polarization effects at material interfaces. For example, in designing optical systems like lenses or mirrors, controlling the tangential component enables engineers to manipulate light paths and focus points.
In electromagnetic waveguides and transmission lines, the tangential electric field component influences mode propagation, impedance matching, and energy transfer characteristics. Engineers use this information to design efficient communication systems, microwave devices, and high-frequency circuits.
Furthermore, when studying scattering and diffraction phenomena, the tangential component of the electric field plays a vital role in analyzing radar signatures, optical diffraction patterns, and acoustic scattering. It provides insights into how waves interact with obstacles, surfaces, and structures, aiding in radar design, imaging systems, and acoustic engineering applications.
In summary, the normal and tangential components of vectors like the electric field are indispensable tools in various physics and engineering scenarios. They help characterize boundary behavior, charge distributions, wave propagation, scattering phenomena, and optical properties, ultimately contributing to the design, analysis, and optimization of a wide range of devices and systems.
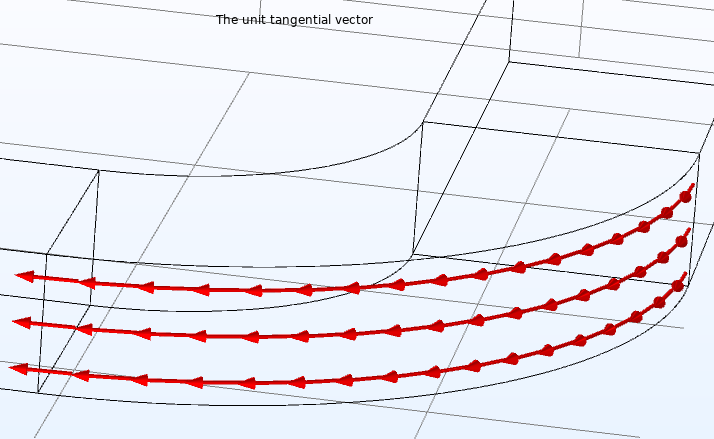
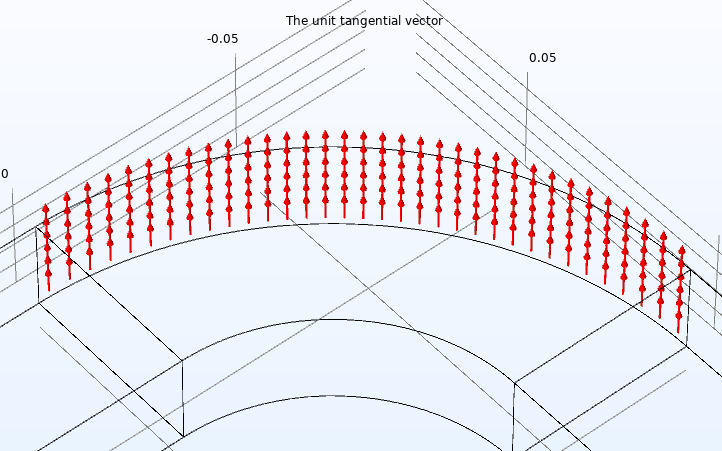
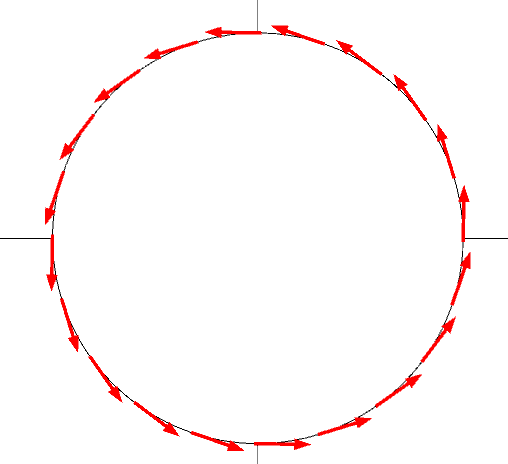
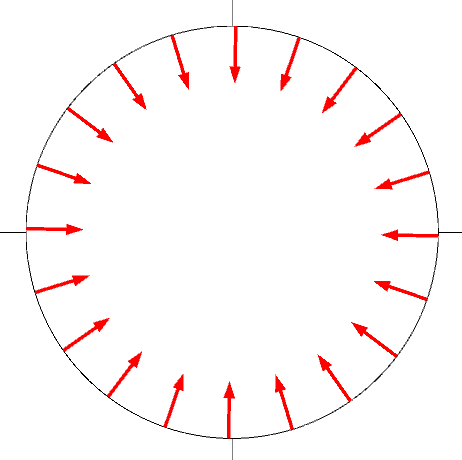
Comsol provide the tangential and normal unit vector fields. The tangential vector is (tx,ty) and the normal vector is (nx,ny) in 2D. The normal vector is (nx,ny,nz) in 3D. There are two tangential vectors (t1x,t1y,t1z) and (t2x,t2y,t2z). The two tangential vectors are perpendicular.
With the help of the unit tangential and normal vector fields, we can get the normal and tangential component fields easily.
`E_bot=E * n=[E_x, E_y, E_z]*[n_x,n_y,n_z]=E_x n_x+E_y n_y +E_z n_z` and
`E_(||)=E-E_bot`
`E_(||)=E * t_1 or E*t_2`
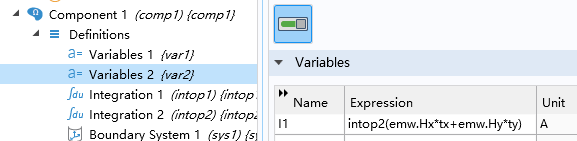
You can use these expresses to plot the normal and tangential components of a field. You can also use these expresses to define local variable before you have a analyse. Local variables are user-defined quantities that can be used within the scope of a specific physics interface or within a particular part of your model. These variables are typically defined using mathematical expressions and can represent parameters, constants, derived quantities, or intermediate results that are relevant to your simulation.
In summary, it is easy to get the normal and tangential component of a field with the help of the unit normal and tangential vector.