Coaxial cable is a type of electrical cable that is widely used in telecommunications and computer networking to transmit data, video, and audio signals. It consists of a central conductor, which is usually made of copper or aluminum, surrounded by a dielectric insulating layer, and then an outer conductor that is typically made of a metal braid or foil. The outer conductor is covered by an insulating layer, and the entire cable is protected by an outer sheath.
Coaxial cables are designed to carry high-frequency signals with low losses, making them suitable for applications such as cable television (CATV), internet connections (via cable modems), satellite communications, and CCTV systems. They offer good shielding against electromagnetic interference (EMI) and radio frequency interference (RFI), which helps maintain signal quality over long distances.
Coaxial cables come in various types and sizes, each designed for specific applications and signal requirements. The connectors used with coaxial cables, such as F-type connectors or BNC connectors, also play a crucial role in ensuring proper signal transmission and connection integrity.
Coaxial cables can carry high power, but the amount of power they can handle depends on several factors such as the cable’s design, construction materials, and operating conditions. Coaxial cables are commonly used to transmit signals with relatively low power levels, such as audio, video, and data signals. However, they can also be used for applications requiring higher power transmission, such as in radio frequency (RF) systems and broadcasting.
The characteristic impedance of a coaxial cable is determined by the ratio of the inner conductor diameter to the outer conductor diameter, the dielectric material between them, and the material properties of the conductors and insulator. It plays a crucial role in ensuring proper signal transmission, impedance matching with connected devices, and minimizing signal reflections that can degrade signal quality.
The electromagnetic field in the coaxial cable
We solve the Maxwell’s equations in cylindrical coordinates for the electric and magnetic field components in a coaxial cable carrying a high-frequency signal in TEM mode. The outer diameter is b and the inner diameter is a. The signal’s angular frequency is ~omega~. We have the following assumptions:
1. \( E_z = E_\phi = H_\rho = H_z = 0 \) (TEM mode).
2. Field components \( E_\rho(\rho, z) = E_{\rho 0}(\rho) e^{j k z} \) and \( H_\phi(\rho, z) = H_{\phi 0}(\rho) e^{j k z} \), where \( k \) is the wavenumber associated with the signal’s frequency.
Gauss’s law for electric fields:
~\nabla \times \vec E=rho/epsilon~
Expand it in cylindrical coordinate, \(\nabla \cdot F = \frac{1}{J}\sum_i\partial_i\Biggl(\frac{J}{h_i}F_i\Biggl)\)
~1/rho del/(del rho) [rho E_(rho0)(rho) e^(-j k z)]=0~
As a result,
~rho E_(rho0)(rho)=C~,
~E_(rho0)(rho)=C/rho~, where C is a constant.
Faraday’s Law
~\nabla \times \vec E=-(delB)/(delt)~
Expand it in cylindrical coordinate and use phasors,
~E_(rho0)(rho)e^(-jkz) (-jk)=-j omega mu H_(phi0)(rho)e^(-jkz)~
Simplify,
~H_(phi0)(rho)=1/Z_0 C/rho~, where Z0 is the wave impedance in the vacuum.
The electromagnetic fields are inversely proportional to the radius. The electromagnetic at the surface of inner conductor is the maximum.
The voltage between the outer and inner conductor is
`V=int_a^b E_(rho0)(rho)drho=int_a^b C/rho drho=Cln(b/a)`
According to the Ampère’s circuital law, the current in the inner conductor is
`I=oint H_(phi0)(a) dl=2 pi a 1/Z_0 C/a=(2 pi C)/Z_0`
We define the characteristics impedance Z as
`Z=V/I=Cln(b/a) Z_0/(2piC)=Z_0/2pi ln(b/a)=60ln(b/a)`
The poynting vector is
`\vec P=1/2 \vec E \times \vec H^*=1/2 C/rho e^(-jkz) \hat e_r\times 1/Z_0 C/rho e^(jkz) \hat e_phi=1/(2Z_0)C^2/rho^2 \hat e_z`
The power is
`P=int int 1/(2Z_0)C^2/rho^2 rho dphi drho=(piC^2) /(Z_0)ln(b/a)`
It is also equal to
`P=1/2 V I=1/2 Cln(b/a) 2piC/Z_0=(piC^2)/Z_0 ln(b/a)`
The power is limited by the maximum electric field in the coaxial cable. The outer conductor is selected. How to choose the inner conductor to get the maximum power?
The maximum electric field `E_c` is on the surface of the inner conductor,
`E_c=C/a`
so `C=a E_c` substitute it into the power formula,
`P=(pi a^2 E_c^2)/Z_0 ln(b/a)`
Derivative it respect to a,
`(dP)/(da)=(pi E_c^2)/Z_0[2aln(b/a)-a]=0`
and 0<a<b,so,
`ln(b/a)=1/2`
`a=b/sqrt(e)`
The characteristics impedance is `Z=60ln(b/a)=30 Omega`
With the critical electric field, we want to get the maximum voltage when the VSWR is very high.
`V=aE_cln(b/a)`
Derivative it respected a
`(dV)/(da)=(-1+ln(b/a))E_c=0`
So,
`ln(b/a)=1`
`a=b/e`
The characteristic impedance is
`Z=60ln(b/a)=60 Omega`
If there is no dielectric material between the inner and outer conductors of the coaxial cable for the high power, then the loss in the cable will primarily be due to ohmic losses in the conductors. Ohmic losses occur due to the resistance of the conductive material, which leads to power dissipation in the form of heat. The formula for calculating the ohmic loss in a coaxial cable is based on the cable’s dimensions, material properties, and the current passing through it. The carried power is
`P=1/2 Z I^2`
And the ohmic loss in the inner and outer conductors is
`P_(loss)=1/2 I^2 r_s/(2pi delta)(1/a+1/b)`
So,
`P_(loss)=Pr_s/Z 1/(2pi delta)(1/a+1/b)=Pr_s/Z_0(1/a+1/b)1/ln(b/a)`
Derivative respected a
`(dP_(loss))/(da)=(Pr_s)/Z_0(-bln(b/a)+a+b)a^2b)=0`
As a>0 and b>0
`-bln(b/a)+a+b=0`
divided by a
`-b/aln(b/a)+1+b/a=0`
This is a equation of b/a, solve it numerically,
`b/a~~3.57`
and the characteristic impedance is
`60ln(b/a)~~60ln(3.57)=76.7 Omega`
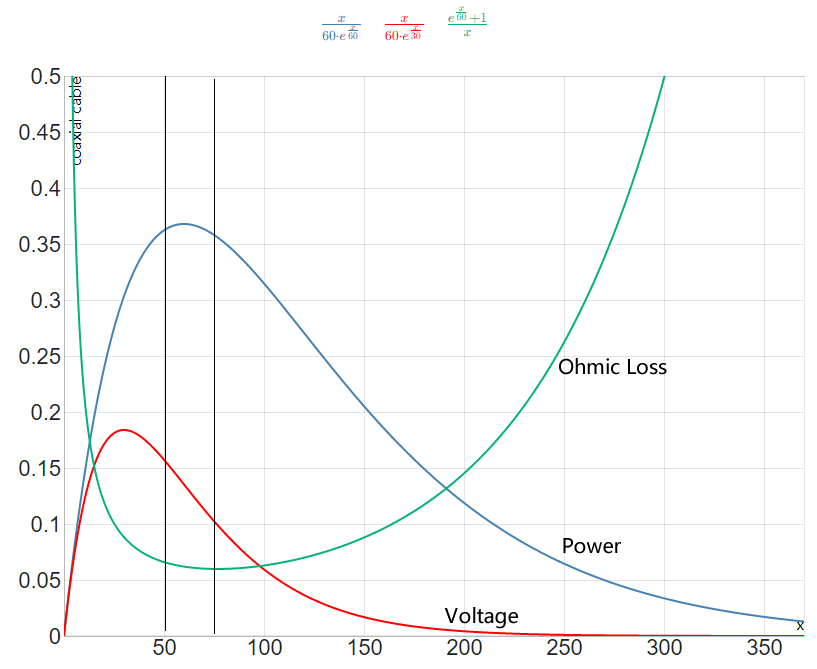
Overall, let the characteristic impedance be a variable and b=1, we have
`ln(b/a)=Z/60` and `a=e^(-Z/60)`
The Voltage is proportional to `aln(b/a)=e^(-Z/60) Z/60`
The Power is proportional to `a^2ln(b/a)=e^(-2Z/60) Z/60`
The Loss is proportional to `(1/a+1/b)/ln(b/a)=(exp(Z/60)+1)*1/Z`
Plot them together,we get this curves.
The standard characteristic impedances of coaxial cables are typically 50 ohms and 75 ohms for historical, practical, and technical reasons. Here’s why these specific values are commonly used:
Historical Significance:
The choice of 50 ohms and 75 ohms as standard characteristic impedances for coaxial cables dates back to the early development of telecommunications and radio frequency (RF) systems. These values were established based on the needs of specific applications and the characteristics of available materials and technologies at the time.
Matching Impedance with Components:
The characteristic impedance of a transmission line plays a crucial role in impedance matching between components such as antennas, transmitters, receivers, and other devices. A well-matched transmission line minimizes signal reflections, optimizes power transfer, and ensures efficient signal transmission.
50 Ohms for RF and Data Transmission:
Coaxial cables with a characteristic impedance of 50 ohms are widely used in RF communications, data transmission (e.g., Ethernet over coaxial), and high-frequency applications. This impedance value provides good impedance matching for many RF systems and supports efficient transmission of signals over a wide frequency range.
75 Ohms for Video and Audio Applications:
Coaxial cables with a characteristic impedance of 75 ohms are commonly used in video and audio applications, including cable television (CATV), satellite TV, and audio/video equipment. This impedance value is well-suited for carrying analog and digital video signals, providing low signal distortion and good impedance matching for multimedia transmission.
Manufacturing Standards and Industry Adoption:
Over time, industry standards and specifications have been established around the use of 50-ohm and 75-ohm coaxial cables for various applications. Manufacturers produce cables, connectors, and other components designed specifically for these impedance values, making it easier for system designers and installers to select and integrate compatible equipment.
Optimized Performance and Loss Characteristics:
The choice of characteristic impedance also takes into account the desired performance characteristics, such as signal loss, attenuation, and interference resistance. The design and construction of coaxial cables for different impedance values are optimized to meet the specific requirements of their intended applications.
Overall, the standard characteristic impedances of coaxial cables reflect a combination of historical practices, technical considerations, industry standards, and compatibility requirements across a range of communication and audio/video systems. 50-ohm is chosen in the high power system.